
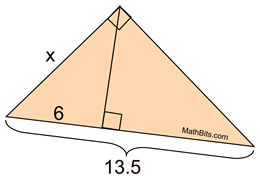
If we consider the hypotenuse and short leg of each, the following ratios of corresponding parts are equal. Notice that d + e = c.Īs an example, consider. In, the length of the hypotenuse is a and the length of is h let e be the length of. Then in, b is the length of the hypotenuse let d be the length of and h the length of, which is the altitude of. These similarities lead to important proportions, which can be more easily represented if we label the sides of the triangles: In, let a be the length of the side opposite angle A, b be the length of the side opposite angle B, and c be the length of the hypotenuse. In the above, the letters are in the order of double-marked angle, right angle, single-marked angle. Notice that the similarities must be named consistently. The altitude to the hypotenuse forms three similar triangles: Triangle ABC is a right triangle with hypotenuse and altitude : In the special case of a right triangle, each leg is an altitude perpendicular to the other leg, and there is a third altitude from the right angle perpendicular to the hypotenuse that plays an important role in measurement The dashed segments,, in the following figures are altitudes of the triangles: So the red line goes from (0,0) to (3.84, 2.88).An altitude of any triangle is a segment that extends from a vertex to the opposite side (or an extension of the opposite side) and is perpendicular to that side. 4/3x + 8 = 3/4x (multiply both sides by 12 to eliminate fractions) To find the point of intersection, we can set the two equations equal to each other: Since its y-intercept is 0, the equation of the red line is: Since the red line is perpendicular to the hypotenuse line, its gradient must be 3/4 (negative reciprocal or m*m = -1). Therefore the equation of the line of the hypotenuse is: Therefore the gradient (slope) is -8/6 = -4/3. The hypotenuse line goes through the points (6,0) and (0,8). So we can set up a proportion with the long legs and the hypotenuses. We know they are similar because they both have an angle of 90 degrees and they share the angle at the point (6,0). I will work with the bottom triangle and the big triangle. The red line divides the big triangle into two smaller triangles, both of which are similar to the big triangle. *note, you could also do this finding the top angle and using the upper triangle formed by the red line In this triangle 6 is the hypotenuse and the red line is the opposite side from the angle we found. We see that this angle is also in a smaller right triangle formed by the red line segment. We know that the legs of the right triangle are 6 and 8, so we can use inverse tan to find the base angle. Pythagoras tells us that the hypotenuse is 10 (6^2 + 8^2 = 10^2), and we already know the area of the triangle is 24, so 24 = 0.5(10)(red line) –> 24 = 5x –> x = 4.8.

So it is also possible to calculate the area by doing 0.5(hypotenuse)(red line).

But the red line segment is also the height of the triangle, since it is perpendicular to the hypotenuse, which can also act as a base. In a right triangle, we can use the legs to calculate this, so 0.5(8)(6) = 24. Here they are given based on the hint question: There are many methods to finding the answer.
Interpreting Categorical and Quantitative Data.Expressing Geometric Properties with Equations.Similarity, Right Triangles, and Trigonometry.Linear, Quadratic, and Exponential Models.Reasoning with Equations and Inequalities.Arithmetic w/ Polynomials & Rational Expressions.


 0 kommentar(er)
0 kommentar(er)
